包阅导读总结
1. 算法、大 O 符号、时间复杂度、空间复杂度、运行时间
2. 本文主要介绍了算法中的大 O 符号,它用于描述算法的效率,包括时间复杂度和空间复杂度,给出了不同复杂度的典型应用,并列举了一些相关的系统设计问题和文章。
3.
– 算法中的大 O 符号
– 用于计算机科学描述算法效率
– 提供运行时间或内存使用量增长速度的上限
– 大 O 符号的主要内容
– 时间复杂度:衡量算法运行时间随输入大小的变化
– 空间复杂度:衡量算法内存使用量随输入大小的变化
– 不同复杂度的示例
– O(1):恒定时间
– O(n):线性时间
– O(log n):对数时间
– O(n^2):二次方时间
– O(n^3):立方时间
– O(n log n):线性对数时间
– O(2^n):指数时间
– O(n!):因式分解时间
– O(sqrt(n)):平方根时间
– 相关系统设计问题和文章
– 8 大系统设计常见问题
– 如何扩展数据库、蜂窝架构等
– 低时延股票交易系统的设计
思维导图: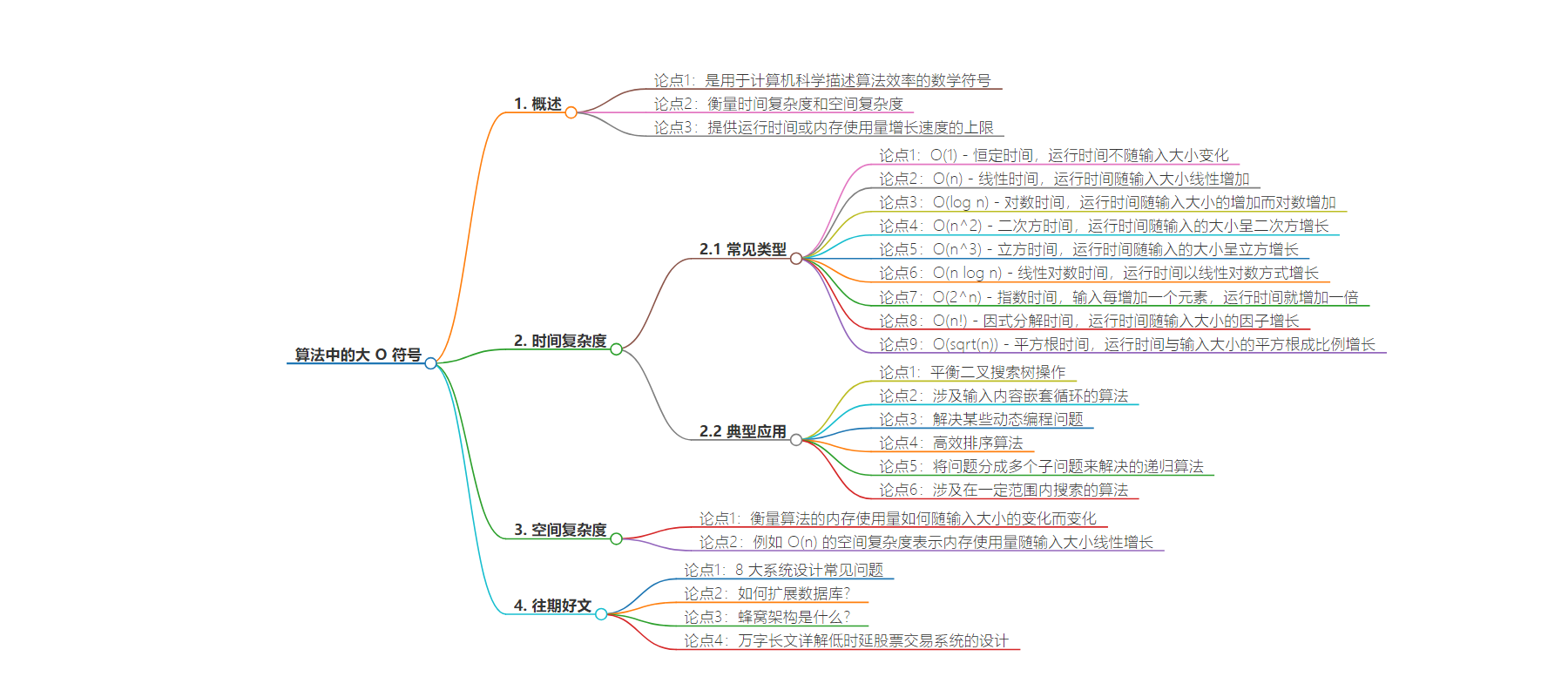
文章地址:https://mp.weixin.qq.com/s/FICu7sl2gbkCVlFZOpBHTA
文章来源:mp.weixin.qq.com
作者:李华
发布时间:2024/8/27 13:21
语言:中文
总字数:954字
预计阅读时间:4分钟
评分:86分
标签:算法,时间复杂度,空间复杂度,计算机科学,数据结构
以下为原文内容
本内容来源于用户推荐转载,旨在分享知识与观点,如有侵权请联系删除 联系邮箱 media@ilingban.com
大 O 符号是一种数学符号,用于计算机科学中描述算法的效率,特别是时间复杂度和空间复杂度。
它提供了一个上限,描述了随着输入数据大小增加,算法的运行时间或内存使用量的增长速度。
大 O 符号主要用于表达以下内容:
-
时间复杂度:衡量算法的运行时间如何随着输入大小的变化而变化。例如,时间复杂度为 O(n) 的算法表示其运行时间随着输入大小的线性增长。 -
空间复杂度:衡量算法的内存使用量如何随着输入大小的变化而变化。例如,空间复杂度为 O(n) 的算法表示其内存使用量随着输入大小的线性增长。
01 O(1) – 恒定时间
运行时间恒定,不随输入大小变化。
典型应用
02 O(n) – 线性时间
运行时间随输入大小线性增加。
典型应用
03 O(log n) – 对数时间
运行时间随输入大小的增加而对数增加。
典型应用
-
平衡二叉搜索树(如 AVL 树、红黑树)上的操作。
04 O(n^2) – 二次方时间
运行时间随输入的大小呈二次方增长。
典型应用
-
涉及输入内容嵌套循环的算法(例如,比较所有元素对)。 -
解决某些动态编程问题,如矩阵链式乘法的 native 实现。
05 O(n^3) – 立方时间
运行时间随输入的大小呈立方增长。
典型应用
-
更复杂的动态编程问题,如 Floyd-Warshall 最短路径算法的天真实现。
06 O(n log n) – 线性时间
运行时间以线性对数方式增长,结合了线性增长和对数增长。
典型应用
-
高效排序算法,如合并排序、快速排序(平均情况)和堆排序。
07 O(2^n) – 指数时间
输入每增加一个元素,运行时间就增加一倍。
典型应用
-
将问题分成多个子问题来解决的递归算法,例如旅行推销员问题的 native 解法。
08 O(n!) – 因式分解时间
运行时间随输入大小的因子增长。
典型应用
09 O(sqrt(n)) – 平方根时间
运行时间与输入大小的平方根成比例增长。
典型应用
-
涉及在一定范围内搜索的算法,如查找 n 以内所有素数的 Eratosthenes 筛法。
——– 往期好文——–
8 大系统设计常见问题
如何扩展数据库?
蜂窝架构是什么?
万字长文详解低时延股票交易系统的设计

