包阅导读总结
1. 关键词:维度、降维升维、表达方法、权衡、复杂问题
2. 总结:本文主要介绍了维度的概念,包括其定义和在不同领域的同义表述,阐述了降维和升维的意义及应用,列举了多种维度表达方式,如象限、向量、矩阵等,并指出在处理问题时要权衡维度,掌握多维度分析方法。
3. 主要内容:
– 维度的定义
– 广义定义:事物“有联系”的抽象概念的数量
– 同义表述:在不同领域与“维度”同义的词汇
– 降维和升维
– 降维:减少复杂度,抓住主要矛盾
– 升维:引入新维度解决两难抉择
– 维度表达
– 象限表示法:两个维度的表达利器
– 向量表示法:用于机器学习,如 Word Embedding
– 矩阵表示法:适合多维度或多维度值的情况
– 总结
– 维度体现事物变化,需权衡维度
– 掌握多维度分析方法解决复杂问题
思维导图: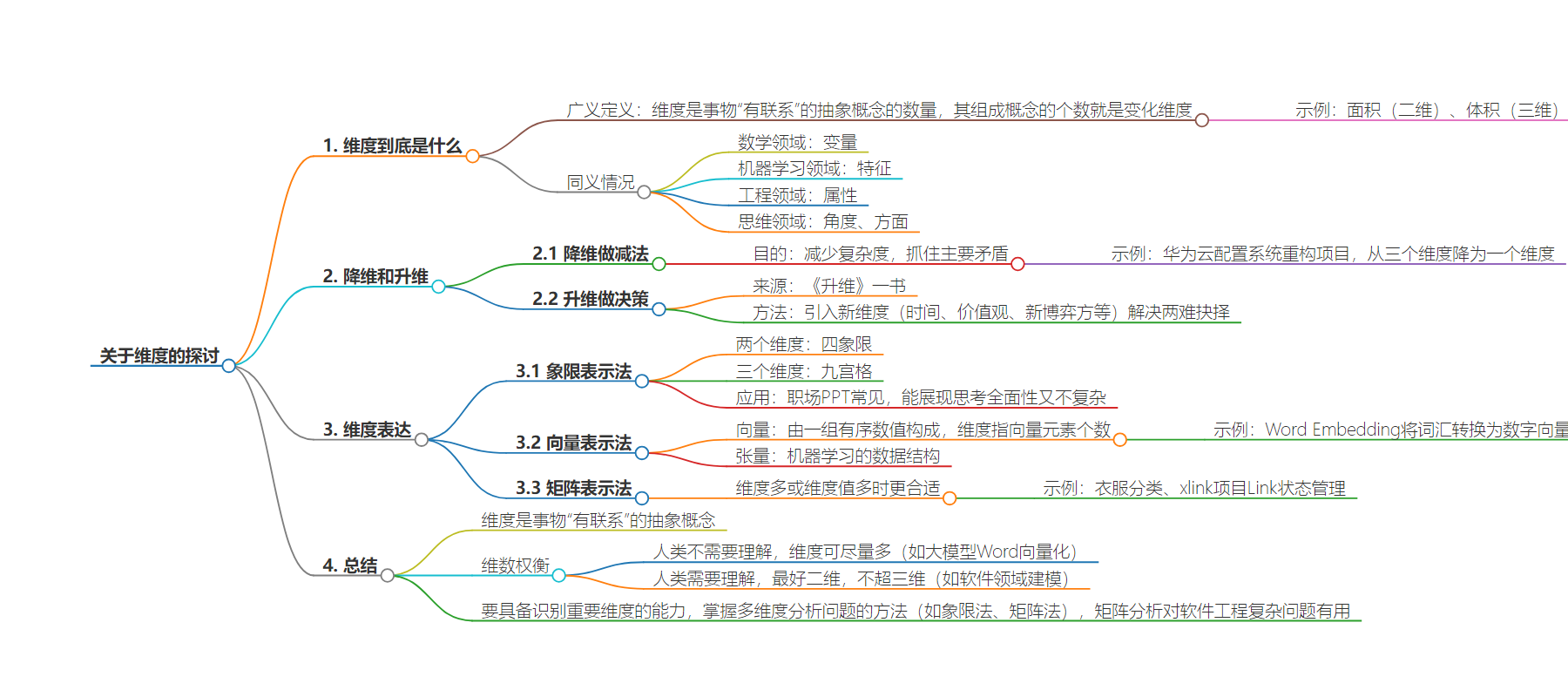
文章地址:https://mp.weixin.qq.com/s/tTGvZIij71C89bZiDjfAvw
文章来源:mp.weixin.qq.com
作者:从码农到工匠
发布时间:2024/7/23 8:11
语言:中文
总字数:4803字
预计阅读时间:20分钟
评分:87分
标签:维度思维,决策分析,复杂系统,矩阵分析,思维方法
以下为原文内容
本内容来源于用户推荐转载,旨在分享知识与观点,如有侵权请联系删除 联系邮箱 media@ilingban.com
维度是一个非常重要的抽象概念,即使我在《程序员的底层思维》花了一章的篇幅专门介绍“维度思维”,也难尽其义。随着LLM大模型的火热,维度、向量这些基础概念变得更加重要,所以非常有必要反刍一下。
1. 维度到底是什么
关于维度的广义定义是这样的:维度是事物“有联系”的抽象概念的数量,“有联系”的抽象概念指和任何一个组成它的抽象概念都有联系,组成它的抽象概念的个数就是它变化的维度。
比如“面积”这个概念是和“长”、“宽”两个抽象概念(变量)相关的,“长”和“宽”的变化都会影响面积的变化,所以它是一个典型的二维问题。体积这个概念涉及到“长”、“宽”、“高”三个变量,是三维的。
上面这个定义还是比较到位的,然而在实际生活中,不管是中文还是英文,语言的模糊性,在“维度”这个概念上都体现的淋漓尽致,比如维度(Dimension)、特征(Feature),变量(Variable)、属性(Attribute),要素(Element)、方面(Aspect)、角度(View)。虽然名称各不相同,但在不同的场合,他们都可能呈现出和“维度”同样的内涵。这也是为什么我会专门研究维度的原因,因为这些同义性曾经给我造成过不少困惑。
根据维度定义出发,它主要表达“事物变化量”的意思,细分一下,至少在以下情况,这些词和“维度”同义:
-
数学领域:变量(Variable),是“变化量”,y=ax + b, 有两个变量,也就是两个维度,典型的二维坐标系平面几何
-
机器学习领域:特征(Feature),特征工程就是提取重要的“变化量”,每个特征都是一个特征维度
-
工程领域:属性(Attribute),一般我们把类(Class)的成员变量也叫属性,即能够引起实例(Instance)不同的变化量;我们说这个系统应该包含哪些要素(Element),等同于说这个组成这个系统的重要元素和维度
-
思维领域:我们说,你要从不同角度(View)看问题;你考虑问题,要考虑到它的方方面面(Aspect),说的就是你是否能全面思考“变化量”的能力。关于这个,我在《程序员的底层思维》中说过,“点线面体”体现了不同的思维维度。单点的看问题很low(点是零维);不会转弯的思维是“一根筋”(一维的);全面的看问题二维的(面积是二维);体系化的思考是三维(体积是三维)
2. 降维和升维
简单来说,维度就是“变化量”。维度越多,变化量越多,对事物的表征越精细充分,同时问题也变得越复杂。维度越少,变化量越少,对事物的表征越简单粗糙,但同时问题也变得简单。又是一个典型的权衡问题:我思考简单,你说我“一根筋”,我思考全面,你说我“太复杂”。权衡的艺术就是中庸之道,即维度太少要升维,维度太多要降维。到底需要多少维度,对于中庸的问题答案只有一个——it depends。
2.1 降维做减法
《三体》里面的降维打击,说的是高维度生物对低维度生物的技术碾压。而现实中的降维,主要是为了减少复杂度,或者说是抓住主要矛盾,放弃次要矛盾,高效解决问题。我第一次和华为云的合作,是关于一个配置系统重构的项目。配置系统作为云平台的关键服务,其重要性不言而喻。在我参与之前,这个项目已经设计了大半年时间,当时的设计如下图所示:
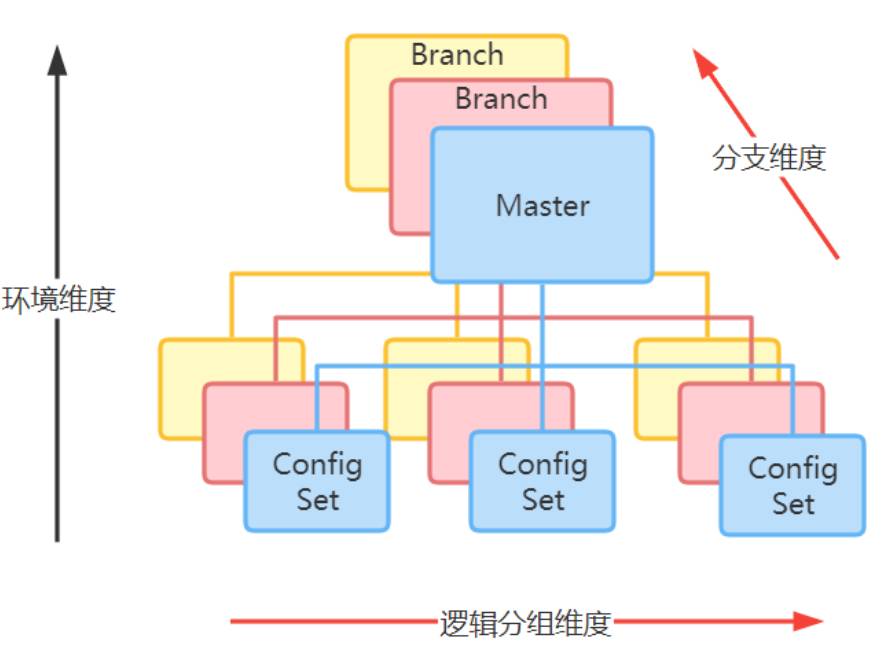
主要是对配置进行了三个维度的设计。
-
借鉴了Git的Master/Branch机制,给每一个配置提供了一个Master版本和多个Branch版本,从而支持配置的并发修改的能力
-
借鉴阿里的Nacos开源配置系统,给配置文件内部提供逻辑分组ConfigSet的能力
-
华为云固有的环境层次维度,也就是Global、Region、AZ、Pod,Cluster那一套。
我觉得我对这个项目最大的贡献,就是在设计阶段,努力说服大家把这三个维度的复杂性降维成一个维度。因为这种最核心模型的维度复杂性,在上层业务中,会被指数级放大。也就是你对配置做任何事情,都需要考虑三个维度的事情:维度一,这个配置是属于哪个环境;维度二, 这个配置是在哪个分支;维度三,这个配置是属于哪个ConfigSet。其复杂度可想而知。详细分析之后,我们发现分支维度、逻辑分组维度都不是必须的,最后我们只保留了环境维度。这个降维决策,至少给项目减少了2/3的复杂度。如果沿用之前的设计,项目很快就会被拖进泥潭,进入噩梦!
2.2 升维做决策
这一节的感触,实际上是来自一本樊登推荐过的书《升维》。这本书的大意是说,只考虑一个维度太简单,太多维度会造成混乱,两个维度的是我们比较容易接受的。在面对两难抉择时,我们必须要引入新的维度(也就是升维)才能撬动局面的改变。就像“布里丹之驴”你必须要推它一把才能做决策。
比如婚姻是一个复杂系统,影响成功婚姻的要素有很多身高、颜值、体型、职业、学历、家庭背景、宗教信仰、个性、品格等等,但如果我们归纳一下,可以把这些要素归纳为人品、财力两个维度——人品和财力,个性、品格、习惯、价值观可以归纳到“人品”里,学历、职业、工资、家庭资产可以归纳为“财力”。
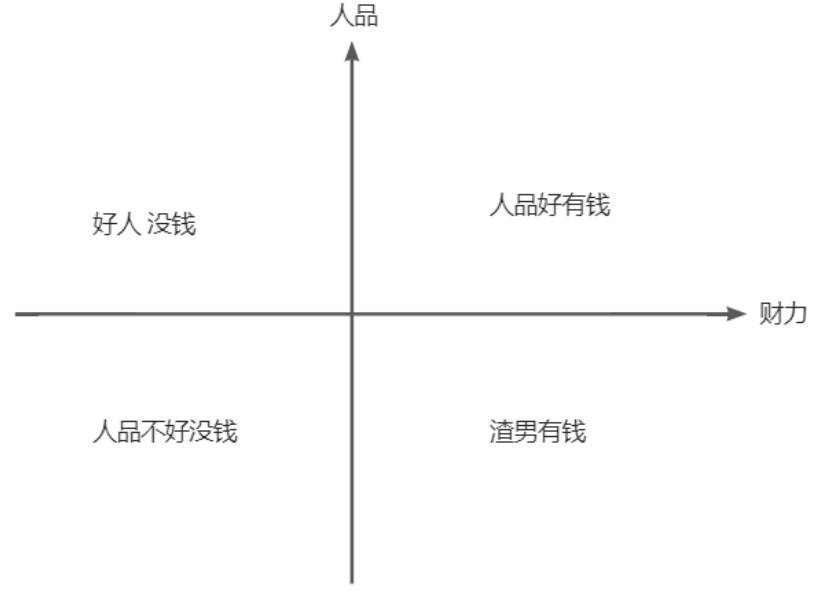
通过这两个关键要素,我们可以构成一个决策矩阵,其中有两个象限不用决策。需要决策的是“在宝马车里哭泣”还是“在自行车上微笑”这个两难局面。不面对两难,就没有到决策的时候,左右为难才要决策。
面对这样的两难局面,我们要做升维思考,即引入新的维度。这个新的维度可以是时间、价值观、新的博弈方等无形化的指标。
解决两难问题,一定不是在当前维度思考,你不可能在当前维度解决当前问题。而是要引入新的维度,新的考量点,从而撬动当前两难的局面,让指针偏向天平的另一方,从而做出决策。
3. 维度表达
从小我们学习平面几何,立体几何。所以会习惯用二维坐标、三维坐标来表达维度。上面介绍的决策矩阵就是典型的二维四象限表示法,除此之外,我们还有很多表达维度的方式。比如在机器学习里面,我们会用向量和张量来表征维度。在分析问题时,通过矩阵展现问题的全貌,是特别有用的方式。在这一节,你会看到对维度的合理表征不仅是重要的数据结构,也是重要的问题分析方法。
3.1 象限表示法
象限法是对两个维度表达,系统化思考的一把利器,在升维里面,我已经给大家展示过如何通过四象限法帮助我们做择偶决策。把维度中的取值,从2个增加到3个,四象限就会转变成九宫格。这个,我在《程序员的底层思维》中也有提到,比如阿里的人才九宫格。就是把人才在价值观和绩效两个维度上进行考核。
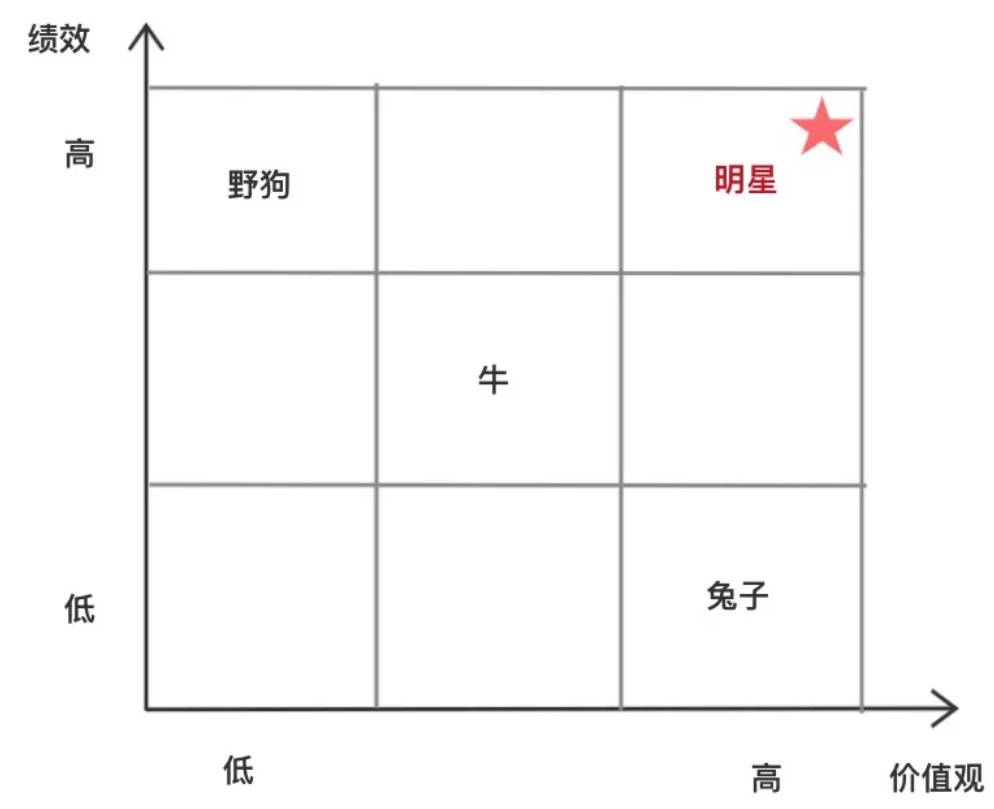
一个维度太简单,多个维度太复杂,对于日常工作中,两个维度的象限表达(或者九宫格)是非常合适的表达方式。既能展现你对问题思考的全面性,也不至于把问题搞的太复杂,别人看不懂。这也是为什么在职场的PPT里面,我们经常可以看到类似的象限展现方式。
3.2 向量表示法
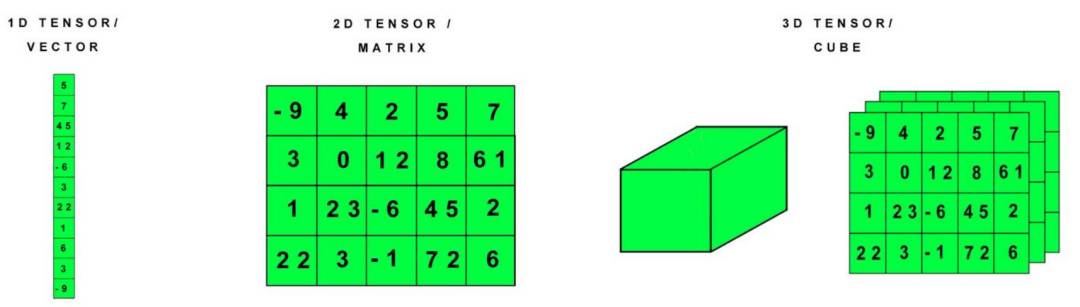
在数学和计算机科学中,向量是由一组有序的数值构成的对象。维度是指向量中的元素个数。n维向量其实是维度(n维)的一个集合,把这n个方面放到了一起{x1,x2,xn}。一个n维向量是一个n维欧式空间(元素是n维向量)的一个点。与向量对应的还有张量(Tensor),张量是机器学习的数据结构,著名的开源机器学习平台TesnorFlow的取名就来自于此。其中一维张量是向量(Vector),二维张量是矩阵(Matrix),三维张量是立方(Cube)
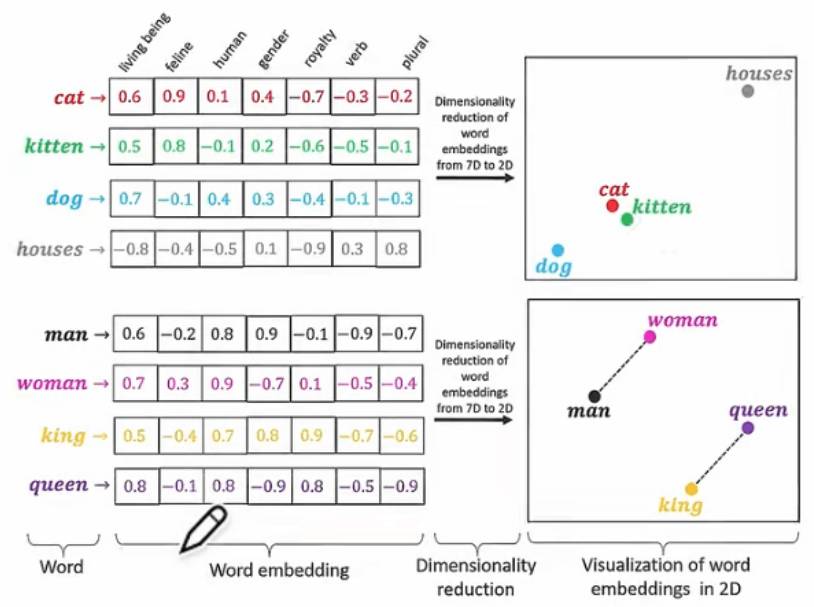
随着大模型的火热,Word Embedding会常常出现,现在的AI的确有不错的智能,但再怎么智能,机器也不会像人一样直接理解文字符号,它只能理解“数字”。Word Embedding就是一项把词汇,转换成数字向量的技术,简单说就是向量化。如下图所示,我们把最右侧的Words,通过Word Embedding转换成有7个维度的向量。这7个维度分别是living being(生物)、feline(猫科)、human(人类)、gender(性别)、royalty(皇室)、verb(动词)、plural(复数)。这7个维度的向量用于表示单词的含义,使得在向量空间中距离较近的单词具有相似的含义。比如cat和kitten相近,women和man相近。
这里只是用7个维度举例子,在一个真实的1000亿参数LLM大模型里面,其模型的向量维度可能在几千到几万维之间,可以说是非常高维度的向量表示。这也是为什么大模型有时候会涌现出令人惊讶的“智慧”的原因,因为如此多维度之间千丝万缕的联系,已经完全超出人类大脑的智力范围。
3.3 矩阵表示法
上文已经介绍过二维四象限和九宫格的表示法。实际上它们也是矩阵,象限是2乘2的矩阵,九宫格是3乘3的矩阵。只是当维度很多,或者维度值很多的时候,矩阵表示法会更加合适。以衣服分类为例,如果只考虑一个季节维度的分类,我们可以这样分:

如果要同时考虑季节、风格两个维度的话,我们可以考虑用树形结构:
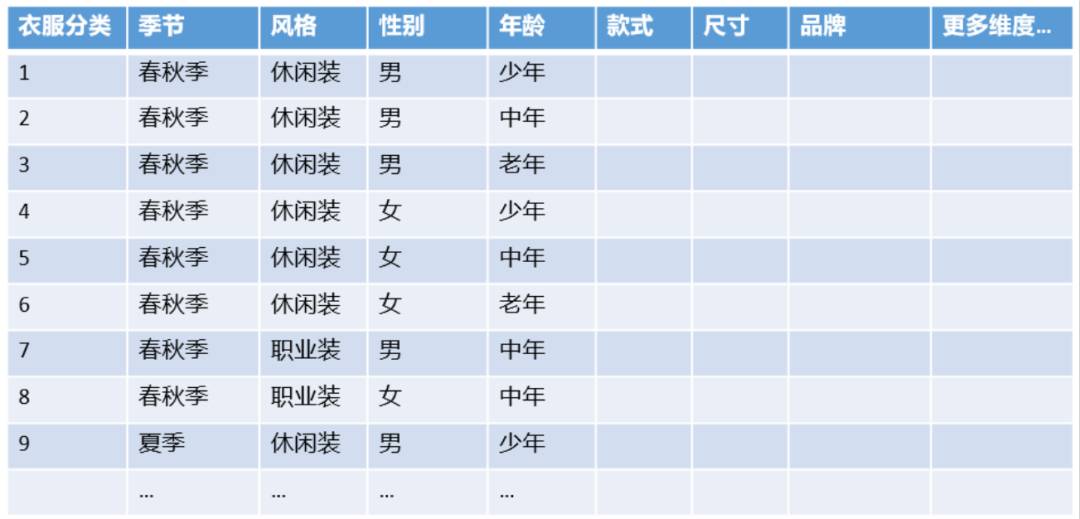
但如果要考虑更多的维度,比如性别、年龄、尺寸、品牌等等,树形枚举就太冗余了,用矩阵来描述会更加清晰。随着维度的增加,分类也会指数级的增加。
再比如,我最近在做的xlink项目,其中最复杂的逻辑要属Link状态管理了,一方面是Link的状态非常多,另一方面是触发Link状态迁移的事件也特别多。对于这样的情况,矩阵分析是看清全貌的一把好手,我们可以把横向维度设置为Link状态,纵向维度设置为Link事件,形成如下的分析矩阵:
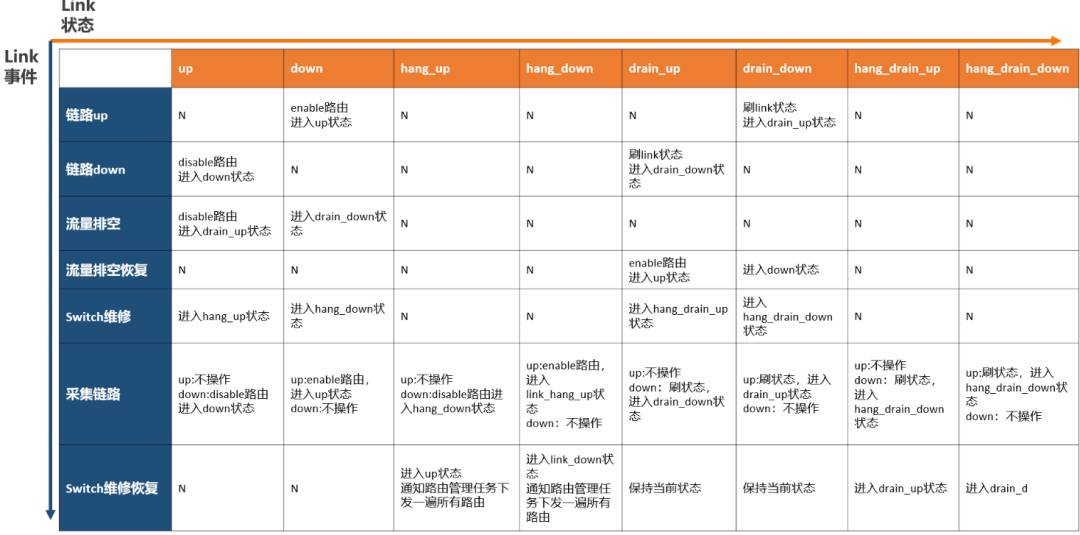
分析清楚之后,我们可以使用cola-statemachine来实现状态转换:
StateMachineBuilder<Status,EventType,Context>
builder=StateMachineBuilderFactory.create();
/**linkup事件**/
builder.externalTransition()
.from(Status.DOWN)
.to(Status.UP)
.on(EventType.link_up)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.DRAIN_DOWN)
.to(Status.DRAIN_UP)
.on(EventType.link_up)
.when(checkCondition())
.perform(doAction());
/**linkdown事件**/
builder.externalTransition()
.from(Status.UP)
.to(Status.DOWN)
.on(EventType.link_down)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.DRAIN_UP)
.to(Status.DRAIN_DOWN)
.on(EventType.link_down)
.when(checkCondition())
.perform(doAction());
/**linkdrain事件**/
builder.externalTransition()
.from(Status.UP)
.to(Status.DRAIN_UP)
.on(EventType.drain)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.DOWN)
.to(Status.DRAIN_DOWN)
.on(EventType.drain)
.when(checkCondition())
.perform(doAction());
/**linkdrainrecovery事件**/
builder.externalTransition()
.from(Status.DRAIN_UP)
.to(Status.UP)
.on(EventType.drain_recovery)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.DRAIN_DOWN)
.to(Status.DOWN)
.on(EventType.drain_recovery)
.when(checkCondition())
.perform(doAction());
/**linkhang事件(包括置维,失连)**/
builder.externalTransition()
.from(Status.UP)
.to(Status.HANG_UP)
.on(EventType.hang)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.DOWN)
.to(Status.HANG_DOWN)
.on(EventType.hang)
.when(checkCondition())
.perform(doAction());
/**linkhangrecovery事件(包括置维,失连)**/
builder.externalTransition()
.from(Status.HANG_UP)
.to(Status.UP)
.on(EventType.hang_recovery)
.when(checkCondition())
.perform(doAction());
builder.externalTransition()
.from(Status.HANG_DOWN)
.to(Status.DOWN)
.on(EventType.hang_recovery)
.when(checkCondition())
.perform(doAction());
builder.internalTransition()
.within(Status.DRAIN_UP)
.on(EventType.hang_recovery)
.when(checkCondition())
.perform(doAction());
builder.internalTransition()
.within(Status.DRAIN_DOWN)
.on(EventType.hang_recovery)
.when(checkCondition())
.perform(doAction());
builder.build(MACHINE_ID);
这样我们把所有的状态转换逻辑,就全部收拢在Statemachine里面,这对于系统的可理解和可维护性非常有好处。我们也可以方便的使用stateMachine.generatePlantUML()生成如下的状态转换图。从而确保设计和实现的一致性。
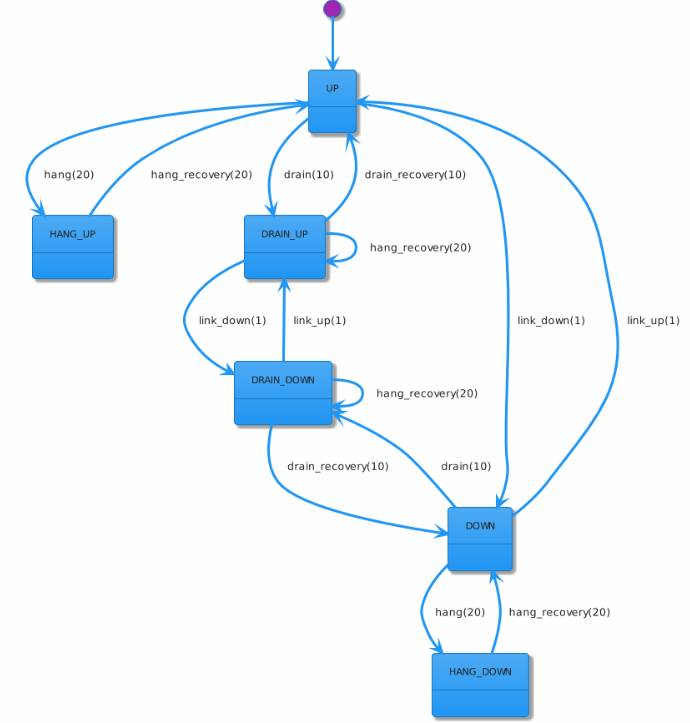
4. 总结
维度,事物“有联系”的抽象概念,体现了事物变化的某个方面。维度的数量反映了我们对事物的认知程度,大多数时候,是高维优于低维。但凡事都有例外,维度越高,事情越复杂。维度越高,模型训练的成本越高。维度越高,人类越难以理解。对于维数的权衡,我认为可以分两种情况:
-
情况一,人类不需要理解,维度可以尽量多。例如大模型的Word向量化的维度,可以尽量大一点,这样可以增大大模型的认知能力
-
情况二,人类需要理解,最好是二维,不要超过三维。比如软件的领域建模,四象限的决策矩阵,多维度的分析矩阵。相比较计算机,人类对多维度的思考能力非常弱,我们的思考对象最好是一维的,超过三维就开始变得难以想象。
这个世界是复杂、多维的,我们不可能时刻都考虑到所有的维度,同时,我们也不能任何时候都是单向度的(One-dimensional)。就像机器学习中的特征工程要选取那些重要的“维度”,我们也要具备识别重要维度的能力,同时对于复杂问题,我们也要掌握多维度分析问题的方法,包括象限法、矩阵法等。对于软件工程中的复杂问题,矩阵分析尤其有用。比如复杂业务场景(维度一),业务流程(维度二)的矩阵分析(参见《程序员的底层思维》的5.3.3)。再比如本文中提到的复杂状态流转,状态(维度一),事件(维度二)的矩阵分析。没有这样的方法论,我们很难看清问题的全貌,也很难无遗漏、全面的分析问题。
